1. 알고리즘 관련 공부
이번 주는 공부했던 알고리즘 지식을 정리하려 한다.

냅색 알고리즘 (Knapsack Algorithm)
- 유명한 다이나믹 프로그래밍 문제 혹은 그리디 알고리즘 문제 중 하나이다.
- 두 가지 유형으로 나뉜다.
- Fractional Knapsack Algorithm: 주어진 자원을 쪼갤 수 있다는 가정 하에 그리디 알고리즘으로 최적의 조건이 구해진다.
- 주어진 조건(ex: 가격, 무게) 중 가장 크거나 작은 것부터 대입하여 최적 방식을 구한다.(그리디 알고리즘)
- 0 - 1 Knapsack Algorithm: 주어진 자원이 0 또는 1, 즉 존재하거나 존재하지 않는, 쪼갤 수 없는 상태면 DP를 사용해야한다.
- 보통 후자의 문제가 자주 나온다. 그래서 쪼갤 수 없는 보석이 나오면 제로원, 디피를 써서 푼다.
- 주로 바텀 업 방식을 사용하나. 주어진 조건을 사용하는 갯수에 제한이 존재한다면 탑 다운 방식을 사용한다.
- Fractional Knapsack Algorithm: 주어진 자원을 쪼갤 수 있다는 가정 하에 그리디 알고리즘으로 최적의 조건이 구해진다.
- 보석 문제를 예로 들자면 memo 리스트(메모이제이션)을 만들어 메모의 인덱스는 무게, 메모의 값은 가치를 넣어 문제를 푼다.
- 여기서 중요한 점은, memo 리스트에 어떤 조건을 값을 쓰고, 어떤 조건을 인덱스를 쓸지 상기해야한다는 것이다.
- 이를 통해 바텀 업으로 접근하는 인덱스에서 주어진 자원의 인덱스 조건을 뺀 값과 주어진 자원의 값을 더한 것을 현재 메모의 값과 비교하여 최대 최소를 정하는 것이다.
- 주어진 조건이 예를 들어 무게 = w, 가치 = v일 때 memo[j] = memo[j-w] + v (최대 가치 수식)
예제) 가방 문제(냅색 알고리즘)
최고 17kg의 무게를 저장할 수 있는 가방이 있다. 그리고 각각 3kg, 4kg, 7kg, 8kg, 9kg의 무게를 가진 5종류의 보석이 있다. 이 보석들의 가치는 각각 4, 5, 10, 11, 13이다.
이 보석을 가방에 담는데 17kg를 넘지 않으면서 최대의 가치가 되도록 하려면 어떻게 담아야 할까요? 각 종류별 보석의 개수는 무한이 많다. 한 종류의 보석을 여러 번 가방에 담을 수 있 다는 뜻입니다.
▣ 입력설명
첫 번째 줄은 보석 종류의 개수와 가방에 담을 수 있는 무게의 한계값이 주어진다. 두 번째 줄부터 각 보석의 무게와 가치가 주어진다.
가방의 저장무게는 1000kg을 넘지 않는다. 보석의 개수는 30개 이내이다.
▣ 출력설명
첫 번째 줄에 가방에 담을 수 있는 보석의 최대가치를 출력한다.
▣ 입력예제 1
4 11
5 12
3 8
6 14
4 8
▣ 출력예제 1
28
해설)
현재 문제에서 메모이제이션은 가방이 된다. 즉 무게가 인덱스가 되고 무게마다 담을 수 있는 최대 가치가 값이 되는 것이다.
메모 리스트의 초기화 값은 문제가 최대의 가치를 구하기 때문에 0으로 값들을 초기화 한다.
여기서 주어진 조건들을 한 줄마다 for문으로 입력 받으면서 무게와 가치로 보석의 데이터를 받는다.
for j in range(n): 을 통해 메모의 인덱스를 접근한다.
메모의 현재 인덱스의 값보다 메모의 현재 인덱스에서 보석의 무게를 뺀 값과 주어진 무게를 더한 값이 크다면 그게 최대가 된다.
물론 계속 보석이 주어지기 때문에 계속 처음 for문이 돌면서 보석들 마다 메모 리스트를 갱신해야한다.
각 보석 당 주어지는 갯수는 무제한이기 때문에 바텀 업으로 갱신이 가능하다.
# 냅색 알고리즘
# 다이나믹 프로그래밍은 메모이제이션에서 담는 값의 의미를 잘 아는 것이 중요하다.
# 현재 문제에서 메모이제이션은 현재 인덱스 j 가방에서 j 무게에 담는 보석의 최대 가치
# j무게가 한계치
# 거기에 담을 수 있는 보석의 최대 가치
# 냅색 알고리즘은 보통 무게가 한정되어 있을 때 담을 수 있는 최대 가치 이런 문제가 나온다.
# 메모 리스트의 인덱스 -> 무게
# 냅색 알고리즘 기본 체계
# 보석의 무게 -> w
# 보석의 가치 -> v
# memo[j] = memo[j-w] + v (최대 가치 수식)
# 하지만 이미 같은 인덱스에 적혀있는 최대 가치가 현재 보석의 상황에서의 최대 가치보다 크다면 그냥 납둔다.
# 반대로 현재 보석의 상황에서의 최대 가치가 더 크다면 바꿔준다.
if __name__ == "__main__":
n,m = map(int,input().split())
# 무게 기준이다, m이 무게이므로 무게의 제한을 두자
memo = [0] * (m+1)
# 보석의 객수 만큼 돌아야한다.
for i in range(n):
w, v = map(int,input().split())
# 현재 보석의 무게부터 시작하자
# 냅색 알고리즘 기본 체계
for j in range(w,m+1):
if memo[j-w] + v > memo[j]:
memo[j] = memo[j-w] + v
print(memo[m])

플로이드 와샬 알고리즘 (Floyd -Warshall Algorithm)
- 냅색 알고리즘을 그래프 최단 거리 문제에 적용한 알고리즘이다.
- '모든 노드'에서 '다른 모든 노드'로 가는 최단 경로를 구할 때 쓰는 알고리즘이다.
- 모든 그래프 문제가 그렇듯 먼저 인접행렬에 값을 넣는다.
- 여기서는 최단 거리를 측정하는 것이기 때문에 가중치가 없는 인접행렬의 값들은 주어진 가중치보다 높은 숫자를 넣는다.
- 가중치가 있으면 가중치를 넣고 없으면 1을 넣는다.
- 중요한 건 방향 그래프는 인접행렬이 비대칭이고 무방향 그래프는 대칭이라는 것이다. 값 입력 받을 때 주의하자
- 여기서 중요한 건 특정 노드에서 다른 노드로 갈 때 중간에 노드를 거쳐간다는 것이기 때문에
- 삼중 for문을 쓴다. 여기서 k는 거쳐가는 노드가 된다.
- for k in range(1,n+1):
- for i in range(1,n+1):
- for j in range(1,n+1);
- for i in range(1,n+1):
- for k in range(1,n+1):
- 특정 노드에서 다른 노드로 갈 때 k가 중간에 들어가기 때문에 memo[i][k] + memo[j][k]가 거쳐가는 값이다.
- 만일 이게 현재 i에서 바로 j로 가는 가중치, 즉 memo[i][j]보다 작다면(최단 거리)
- memo[i][j] = memo[i][k] + memo[j][k]로 값을 갱신한다.
- 삼중 for문이 돌기 때문에 1부터 n번 노드까지 현재 노드가 중간에 거쳐가는 노드일 때의 경우를 전부 갱신할 것이다.
예제) 플로이드 워샬 알고리즘
N개의 도시가 주어지고, 각 도시들을 연결하는 도로와 해당 도로를 통행하는 비용이 주어질 때 모든 도시에서 모든 도시로 이동하는데 쓰이는 비용의 최소값을 구하는 프로그램을 작성하세요.
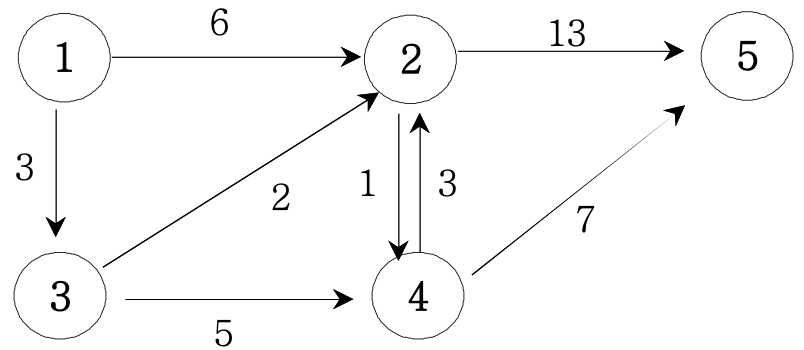
▣ 입력설명
첫 번째 줄에는 도시의 수N(N<=100)과 도로수 M(M<=200)가 주어지고, M줄에 걸쳐 도로정보 와 비용(20 이하의 자연수)이 주어진다. 만약 1번 도시와 2번도시가 연결되고 그 비용이 13이 면 “1 2 13”으로 주어진다.
▣ 출력설명
모든 도시에서 모든 도시로 이동하는데 드는 최소 비용을 아래와 같이 출력한다.
자기자신으로 가는 비용은 0입니다. i번 정점에서 j번 정점으로 갈 수 없을 때는 비용을 “M"으 로 출력합니다.
▣ 입력예제 1
5 8
1 2 6
1 3 3
3 2 2
2 4 1
2 5 13
3 4 5
4 2 3
4 5 7
▣ 출력예제 1
0 5 3 6 13
M 2 0 3 10
M 3 M 0 7
M M M M 0
//1번 정점에서 2번정점으로 5, 1에서 3번 정점으로 3, 1에서 4번 정점으로 6...... M 0 M 1 8 //2번 정점에서 1번 정점으로 갈수 없으므로 “M", .......
# 플로이드 와샬도 냅색 알고리즘과 동일한 원리이다.
# 냅색과 같이 기존 값이랑 경우를 더해서 비교한다.
# 인접행렬을 초기화한다.
# 맨 처음에 들어오는 값들은 노드에서 다른 노드로 직행하는 값
# 이후에 0,0을 제외하고 다 큰 값을 넣어 최솟값 도출을 위해 정리한다.
# i노드에서 j노드로 갈 때 k노드를 거쳐서 가는 비용식
# => board[i][k] + board[k][j]
# 현재 노드에서 타겟 노드로 직행하는 것 vs i노드에서 j노드로 갈 때 k노드를 거쳐서 가기
# 이 두 가지 케이스를 비교해서 더 작은 값을 갱신한다.
# board[i][j] = min(board[i][j], board[i][k] + board[k][j])
# 다이나믹 테이블(메모)에서 순서는 순열이 적용이 된다.
# 즉 순서가 상관이 없다는 뜻이다. 어차피 최소 경로, 즉 제일 좋은 순서대로 메모가 채워진다.
# 어차피 n,n은 자기 자신으로 가는 값으로 기본적으로 0이다.
# 그래서 동적으로 프로그래밍이 될 때 예를 들어 5 -3 - 3이라고 해도
# 결국 5 - 3만 적용이 된다.
if __name__ == "__main__":
n, m = map(int,input().split())
board = [[2147000000]*(n+1) for _ in range(n+1)]
for i in range(1,n+1):
board[i][i] = 0
# for x in range(n+1):
# print(board[x])
# print()
for _ in range(m):
x,y,v = map(int,input().split())
board[x][y] = v
# 중간에 거치는 노드 k가 필요하기 때문에 결국 3중 for문을 돌아야 한다.
for k in range(1,n+1):
for i in range(1,n+1):
for j in range(1,n+1):
if board[i][j] > board[i][k] + board[k][j]:
board[i][j] = board[i][k] + board[k][j]
for i in range(1,n+1):
for j in range(1,n+1):
if board[i][j] == 2147000000:
print("M", end=" ")
else:
print(board[i][j], end=" ")
print()


