1. 알고리즘 관련 공부
이번 주는 공부했던 알고리즘 지식을 정리하려 한다.
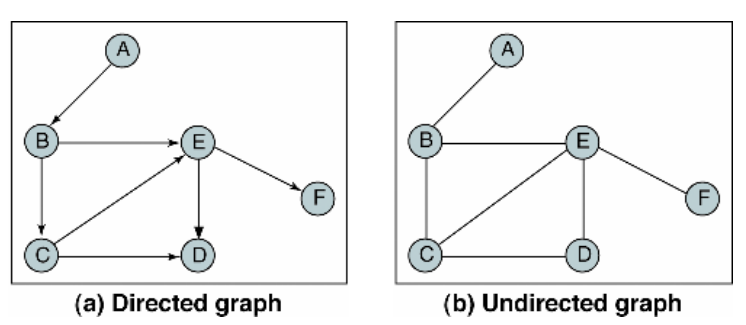
그래프
- 노드와 간선의 집합
- 방향이 설정되어 있으면 방향 그래프
- 방향이 설정되어 있지 않으면 무방향 그래프
- 간선에 값이 설정되어 있으면 가중치를 뜻한다. 이러한 그래프는 가중치 방향 그래프라 한다.
인접 행렬
- 프로그래밍에서 그래프를 표현할 때 사용하는 행렬
- 기본적으로 인접행렬을 입력할 떄 행 -> 열의 방향으로 그래프가 진행 된다고 보면 된다.
- 노드 a가 b로 갈 때 인접 그래프가 g라고 하면 g[a][b] = 1 이렇게 표현한다.
- 가중치가 있으면 g[a][b] = (가중치) 라고 표현한다.
- 무방향 그래프의 경우 g[a][b] = 1 , g[b][a] = 1 이렇게 행과 열을 바꾸어 두 번 지정해주어야 한다.
방문 체크 리스트
- dfs 혹은 bfs를 사용하면 기본 적으로 사용하는 체크 리스트
- 노드에 방문을 했는지 체크하는 리스트로 방문을 안 했다면 값이 0이고 방문을 했다면 1로 값을 지정한다.
- dfs를 사용할 때 백트래킹을 걸어 줄 것이면
- check[i] = 1
- dfs(s)
- check[i]=0
- 이렇듯이 다음 dfs가 메모리 스택에 저장되어 있는 다음 순서에 체크를 미방문으로 해주어야 백트래킹이 된다.
예제) 인접 행렬(가중치 방향 그래프)
아래 그림과 같은 그래프 정보를 인접행렬로 표현해보세요.

▣ 입력설명
첫째 줄에는 정점의 수 N(2<=N<=20)와 간선의 수 M가 주어진다.
그 다음부터 M줄에 걸쳐 연결정보와 거리비용이 주어진다.
▣ 출력설명
인접행렬을 출력하세요.
▣ 입력예제 1
6 9
1 2 7
1 3 4
2 1 2
2 3 5
2 5 5
3 4 5
4 2 2
4 5 5
6 4 5
▣ 출력예제1
0 7 4 0 0 0
2 0 5 0 5 0
0 0 0 5 0 0
0 2 0 0 5 0
0 0 0 0 0 0
0 0 0 5 0 0
해설)
이 문제의 경우 인접행렬을 표현하는 것을 물어보는 기초적인 문제로 위에 적은 인접행렬의 개념과 가중치를 지정하는 표현 방식을 생각하면 된다. 다만 좌표가 1 부터 n 까지인지, 0 부터 n-1 까지인지를 유념하면서 인접행렬을 초기화하고 그에 따른 출력 방법도 달라져야 할 것이다. 가장 간단한 그래프 문제이므로 무방향 그래프 표현 방식도 주석으로 넣어 놨다.
# 그래프 - 노드와 간선의 집합
# 방향이 설정되어 있으면 방향 그래프
# 간선의 값까지 설정되어 있으면 가중치 방향 그래프
# 무방향 그래프, 가중치 방향 그래프 순서로 해볼 것이다.
# 인접 행렬을 통해 그래프를 표현한다.
# 행 -> 열 방향으로 된다고 알아야한다.
# 인접그래프가 g라고 하면
# g[a][b] = 1 이렇게 표현한다.
# 그러면 a -> b 이렇게 간다는 것을 표현할 수 있다.
# 무방향 그래프는 a -> b, b -> a 이렇게 두 곳을 1로 해야한다.
# g[a][b] = 1 , g[b][a] 하나씩 해가는 거다.
# 무방향 그래프 그리기
# n,m = map(int, input().split())
# # 행렬 표현식 외워두자 n이 주어진다면 n+1을 범위로 잡는다.
# # 1 부터 n까지 돌 거다.
# g=[[0]*(n+1) for _ in range(n+1)]
# for i in range(m):
# a,b = map(int, input().split())
# # 무방향 그래프
# g[a][b] = 1
# g[b][a] = 1
# for i in range(1,n+1):
# for j in range(1,n+1):
# print(g[i][j], end=' ')
# print()
# 문제 해결
n,m = map(int, input().split())
# 행렬 표현식 외워두자 n이 주어진다면 n+1을 범위로 잡는다.
# 1 부터 n까지 돌 거다.
g=[[0]*(n+1) for _ in range(n+1)]
for i in range(m):
a,b,c = map(int, input().split())
# 단방향 그래프와 가중치 설정
g[a][b] = c
for i in range(1,n+1):
for j in range(1,n+1):
print(g[i][j], end=' ')
print()
예제) 경로 탐색(그래프 DFS)
방향그래프가 주어지면 1번 정점에서 N번 정점으로 가는 모든 경로의 가지 수를 출력하는 프로그램을 작성하세요.
아래 그래프에서 1번 정점에서 5번 정점으로 가는 가지 수는

1 2 3 4 5
1 2 5
1 3 4 2 5
1 3 4 5
1 4 2 5
1 4 5
총 6 가지입니다.
그래프에서 경로를 방문한 노드는 중복해서 방문하지 않습니다.
▣ 입력설명
첫째 줄에는 정점의 수 N(2<=N<=20)와 간선의 수 M가 주어진다. 그 다음부터 M줄에 걸쳐 연 결정보가 주어진다.
▣ 출력설명
총 가지수를 출력한다.
▣ 입력예제 1
5 9
1 2
1 3
1 4
2 1
2 3
2 5
3 4
4 2
4 5
▣ 출력예제 1 6
해설)
위에서 연습한 인접행렬과 방문 체크 리스트를 가지고 만드는 DFS() 문제다. 경로 탐색은 DFS()를 사용해야하는 것을 잊지 말자.
인식해야될 조건은 1. 방향 그래프, 2. 가중치 없음, 3. 출발 노드는 1 이다.
정지 조건은 방문한 노드가 최종 노드일 때다. 즉 V == N이다. 전에 풀었던 문제들도 기본적으로 L == N 즉, 레벨이 N이 될 때였다.
여기서도 방문 가능한 노드를 찾아야 하기에 else문에서 for문을 돌리면서 다른 노드가 현재 노드와 이어져 있는지 and 방문을 했는 지를 보고 나서 방문하고, DFS(), 방문 취소 이런 로직을 넣어줘야한다.
# 방문 체크 리스트 , 인접 행렬 두 개가 필요하다.
# 경로 탐색은 DFS()를 사용해야한다.
def DFS(v):
global cnt
# 목적 노드에 도착했다면 DFS() 정지
if v==n:
cnt+=1
# 도착했을 때 경로 리스트에 저장된 노드를 다 뽑자
for x in path:
print(x, end=" ")
print()
else: # 가지(상태 노드) 뻗기
for i in range(1,n+1): # i가 방문하려는 노드다. 1부터 5까지
# 방문 로직
# 인접행렬이 연결이 되어있습니까?
if g[v][i] == 1:
if ch[i] == 0:
ch[i] = 1
# i로 가야하니까 i를 경로 리스트에 추가
path.append(i)
DFS(i)
# 백트래킹
path.pop() # 넣었던 거 다시 빼야 백트래킹 된다.
ch[i] = 0
if __name__=='__main__':
n,m = map(int, input().split())
# 인접 리스트 생성
g = [[0]*(n+1) for _ in range(n+1)]
# 방문 체크 리스트 생성
ch = [0]*(n+1)
for i in range(m):
a,b = map(int,input().split())
# 방향 그래프니까 a,b만. 중요!
g[a][b] = 1
cnt = 0
# 방문 경로
path = []
# 방문 시작 노드는 체크해주자
ch[1] = 1
path.append(1)
DFS(1)
print(cnt)

