1. 알고리즘 관련 공부
이번 주는 공부했던 알고리즘 지식을 정리하려 한다.

BFS(Breadth First Searching) 너비 우선 탐색
- 너비 우선 탐색으로 상태트리나 다른 그래프에 있어 같은 레벨에 있는 노드를 우선 적으로 탐색하는 알고리즘이다.
- BFS를 사용할 때는 큐(선입선출) 자료구조를 사용하여 현재 노드를 popleft()하고 현재 노드와 연결된 다음 노드들을 append 한다.
- DFS()와의 차이점은 DFS는 한 루트(시작 노드부터 끝 레벨의 노드까지)를 중점으로 가지 치기를 하는데 사용한다는 점이다.
- 반면 BFS() 현재 노드와 가장 가깝게 연결된 다음 노드들을 레벨 별로 묶어서 최단 경로 찾기와 같은 좌표 이동에 주로 사용한다.
- BFS()는 좌표 관련 문제에서 꽤나 자주 사용하는 편이므로 숙지해야한다.
- 이것 또한 DFS()와 마찬가지로 체크리스트를 만들어야하며 그 외에 데이터 값을 넣을 정보 리스트가 필요하다.
예제) 송아지 찾기(BFS)
현수는 송아지를 잃어버렸다. 다행히 송아지에는 위치추적기가 달려 있다. 현수의 위치와 송아 지의 위치가 직선상의 좌표 점으로 주어지면 현수는 현재 위치에서 송아지의 위치까지 다음과 같은 방법으로 이동한다.
현수는 스카이 콩콩을 타고 가는데 한 번의 점프로 앞으로 1, 뒤로 1, 앞으로 5를 이동할 수 있다. 최소 몇 번의 점프로 현수가 송아지의 위치까지 갈 수 있는지 구하는 프로그램을 작성 하세요.
▣ 입력설명
첫 번째 줄에 현수의 위치 S와 송아지의 위치 E가 주어진다. 직선의 좌표 점은 1부터 10,000 까지이다.
▣ 출력설명
점프의 최소횟수를 구한다.
▣ 입력예제 1
5 14
▣ 출력예제 1
3
해설)
이 문제의 경우 수직선 상으로 보며 상태 트리를 1. 앞으로 1, 2. 뒤로 1, 3. 앞으로 5 이렇게 3개의 노드로 뻗어나간다는 것을 알 수 있다.
수직선 상에서 S와 E 사이에서 움직인다고 보아야하며 dis라는 움직인 횟수를 저장하는 리스트가 필요하다.
거리의 차이는 인덱스를 통해 계산이 가능하다. 일단 dis 리스트를 0부터 10,000으로 크기를 지정하고 모두 0으로 초기화 한다.
이후 주어진 S와 E를 가지고 S를 방문하면서 이동한 값을 0으로 두고 움직일 때마다 BFS()에 sum을 넘겨주며 +1을 계속하면 된다.
최종적으로 BFS()의 정지 조건으로 좌표가 E가 될 때 마지막으로 넘긴 값을 리턴하면 된다.
# 큐를 쓰려면 콜렉션에서 디큐를 임포트 해야한다.
from collections import deque
# BFS(넓이 우선 탐색)
# -> 큐를 이용하는 탐색
# BFS은 레벨 우선 탐색을 한다.
#
# 0
# / \
# 1 2
# / \ / \
# 3 4 5 6
#
# 위의 이진 트리에서 BFS는 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6
# 위와 같이 같은 레벨에 있는 노드를 우선 탐색한다.
# BFS는 큐를 이용한다. 선입선출, 큐에 0번을 넣고 pop()을 해서 연결된 1과 2를 넣는다.
# 그 다음에 1을 pop()하고 1과 연결된 3과 4를 넣는다.
# 그 다음 2를 pop()하고 2와 연결된 5와 6을 넣는다.
# 이 문제에서 상태 트리는 1. 앞으로 1, 2. 앞으로 2, 3. 앞으로 5다.
# 위와 같이 상태 트리의 노드는 3개가 된다.
# 값이 주어지면 그 값에 상태 변화를 가한 3 노드를 상태트리로 지정해야한다.
# 이 문제에서는 dis라는 움직힌 횟수를 표현한 리스트가 필요하다.
# 인덱스에 따라 지점을 방문하면 전 지점의 값에 1을 더한다.
# 방문 리스트도 필요하다. 방문하지 않은 지점에서 다시 방문한 지점으로 갈 이유가 없다.
MAX = 100000
# 0번부터 생기기 때문에 MAX+1
# 체크리스트
ch = [0] * (MAX + 1)
# 거리리스트
dis = [0] * (MAX + 1)
# n = 시작 노드, m = 도착 노드
n,m = map(int, input().split())
# 시작노드 방문
ch[n] = 1
# 현재 움직인 횟수는 0
dis[n] = 0
# 디큐 사용
dQ = deque()
dQ.append(n)
# BFS의 기본 정지 조건은 큐에 값이 남아있지 않을 떄다.
while dQ:
# now는 지금 큐 맨 앞의 값
now = dQ.popleft()
# 문제에서 주어진 정지 조건, 목적지 도착
if now == m:
break
# next는 now의 자식 노드들이다.
# in(데이터,데이터,데이테...)의 표현식도 알아두자.
# 이러면 in()안에 있는 갯수만큼 돈다.
for next in(now-1,now+1,now+5):
# 음수 좌표는 가면 안된다.
if MAX>= next > 0:
# 방문을 했던 곳은 가면 안된다.
# 움직인 최소 값을 찾아야하기 때문에 다시 돌아가는 루트는 필요가 없는 것이다.
if ch[next] == 0:
dQ.append(next)
# 방문 체크
ch[next] = 1
# 움직인 횟수 체크
# 전 노드의 움직인 횟수 + 1
dis[next] = dis[now] + 1
print(dis[m])
예제) 사과나무(BFS)
현수의 농장은 N*N 격자판으로 이루어져 있으며, 각 격자안에는 한 그루의 사과나무가 심어저 있다. N의 크기는 항상 홀수이다. 가을이 되어 사과를 수확해야 하는데 현수는 격자판안의 사과를 수확할 때 다이아몬드 모양의 격자판만 수확하고 나머지 격자안의 사과는 새들을 위해서 남겨놓는다.
만약 N이 5이면 아래 그림과 같이 진한 부분의 사과를 수확한다.
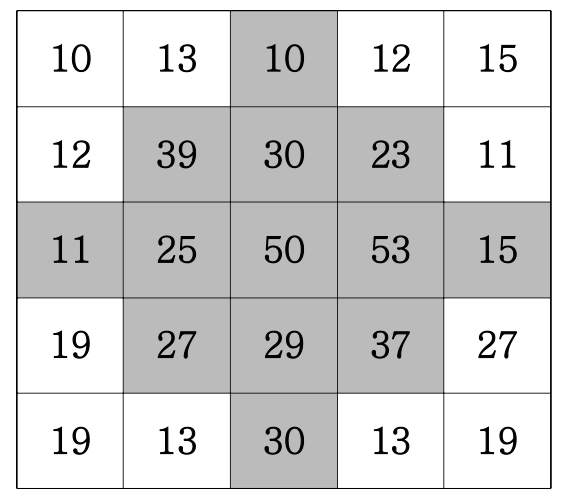
현수과 수확하는 사과의 총 개수를 출력하세요.
▣ 입력설명
첫 줄에 자연수 N(홀수)이 주어진다.(3<=N<=20)
두 번째 줄부터 N줄에 걸쳐 각 줄에 N개의 자연수가 주어진다. 이 자연수는 각 격자안에 있는 사과나무에 열린 사과의 개수이다. 각 격자안의 사과의 개수는 100을 넘지 않는다.
▣ 출력설명
수확한 사과의 총 개수를 출력합니다.
▣ 입력예제 1
5
10 13 10 12 15
12 39 30 23 11
11 25 50 53 15
19 27 29 37 27
19 13 30 13 19
▣ 출력예제 1
379
해설)
이 문제의 경우 투 포인터 전략으로 s와 e 이 두 개의 포인터로 행이 n//2 전까지는 서로 멀어지다 n//2가 넘어간 후 다시 줄어드는 방법으로 풀 수 있지만 BFS()로 푸는 것이 더 빠르다. 행과 열이 n//2인 정 가운데 좌표(노드)에서 시작하여 가장 가까이 있는 노드 상 하 좌 우 4개를 같은 레벨로 보고 탐색하고 그 후 그 노드들의 상 하 좌 우 들을 같은 레벨로 보며 BFS()를 돌려서 풀 수 있다.

이를 리스트로 체계화 시키면 dx = [-1, 0, 1, 0] , dy = [0, 1, 0, -1] 로 나누어 for i in range(4)에서 인덱스로 참조하여 쓸 수 있다.
좌표 문제에서 매번 사용하기 때문에 외워두면 좋을 것이다.
이 문제는 해설 글로 설명하기에는 많은 요소가 포함되어 있기에 주석으로 코드를 파악하기 바란다.
또한 투 포인터 전략도 함께 올려 놓겠다.
BFS 해결법
from collections import deque
# 주어진 n을 //2로 정 가운데 좌표(n//2,n//2)를 지정한다.
# 이후 인접한 노드들을 탐색하면서 이동한다.
# 레벨이 같은 것들을 우선 탐색하기 때문에 BFS로 풀자
# 레벨이 같은 상,하,좌,우가 노드가 된다.
# (2,2) 레벨은 0
# / | | \
# 상 우 하 좌
# (1,2) (2,3) (3,2) (2,1) 레벨은 1
# 이런 좌표 이동은 dx와 dy로 미리 좌표에 적용할 계산들을 리스트를 만들어 두자
# 시계방향이다.
# dx = [-1,0,1,0]
# dy = [0,1,0,-1]
# 방문한 곳을 재방문 안 한다. -> 체크리스트
dx = [-1,0,1,0]
dy = [0,1,0,-1]
# 좌표 생성
n = int(input())
a =[]
for _ in range(n):
lst = list(map(int, input().split()))
a.append(lst)
# 합 초기화
sum = 0
# 방문 리스트
ch = [[0]*n for _ in range(n)]
# 큐 생성
Q = deque()
# 이게 한 세트다 아래에서 똑같이 쓸것
# 맨 위 노드 방문
ch[n//2][n//2] = 1
sum = sum + a[n//2][n//2]
# 큐에 넣기, 노드 자체는 좌표(튜플)로 넣는다.
Q.append((n//2,n//2))
# 레벨 초기화
L = 0
# BFS 로직
# 무한 루프, 후에 탈출할 거임
while True:
# 정지 조건, 중앙에서 출발하니 n//2의 레벨이 된다는 걸 명심하자
if L == n//2:
# 정지
break
# 큐의 사이즈를 저장, 현재 레벨의 노드들이 저장되었을 것
size = len(Q)
# 현재 레벨 전체의 시퀀스
# 현재 레벨의 사이즈 * 4 만큼 돌 것이다.
for _ in range(size):
temp = Q.popleft()
for i in range(4):
# 튜플로 넣었으니까 좌표 입력 가능하다.
# 좌표 도출
x = temp[0] + dx[i]
y = temp[1] + dy[i]
# 방문 체크
if ch[x][y] == 0:
ch[x][y] = 1
sum += a[x][y]
Q.append((x,y))
# 출력
# print(L,size)
# for x in ch:
# print(x)
L = L + 1
# 진짜 합 출력
print(sum)
투 포인터 해결법
n = int(input())
a =[]
for _ in range(n):
lst = list(map(int, input().split()))
a.append(lst)
# 투 포인터 전략
res = 0
s=e=n//2
for i in range(n):
# 핵심 로직, 위에서 아래로 간다고 생각해야한다.
for j in range(s,e+1):
res+= a[i][j]
if i<n//2:
s-=1
e+=1
else:
s+=1
e-=1
print(res)


